ANCIENNES HYPOTHESES 

ET GRANDES DECOUVERTES DE L'ASTRONOMIE

DE POSITION

LES THEORIES

Les Grecs et leurs précurseurs :

Selon une croyance égyptienne, 1 500  ans avant J.-C. la déesse du ciel donnait naissance chaque jour au Soleil et aux étoiles. Un modèle grec, décrit par Thalès aux environs de 600 an. J.-C., montrait une terre plate au centre du système, entourée par la mer et une vaste sphère portant les étoiles et effectuant en un jour, une révolution autour d'un axe passant par le Pôle. Pour rendre compte des mouvements du Soleil, de la Lune et des planètes. Thalès les supposait se mouvoir en sens inverse sur la face intérieure de la sphère.

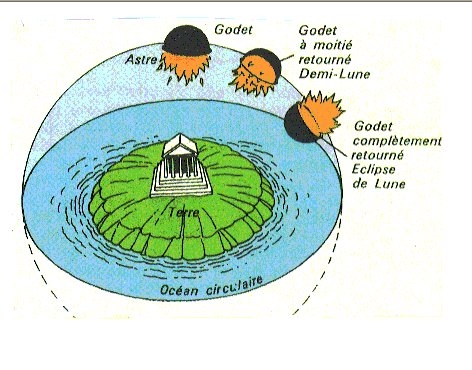
Cosmologie de Thalès de Milet 

L'Ecole pythagoricienne, environ 500 av. J.-C., supposait que la Terre était sphérique, plutôt que plate, et, de ce fait, au centre d'une série de sphères concentriques. La sphère extérieure entraînait les étoiles dans son mouvement. A l'intérieur, se trouvaient d'autres sphères portant la Lune, le Soleil et les planètes. On pensai que toutes les sphères intérieures étaient liées à la sphère extérieure, si bien que tout l'ensemble faisait un tour par vingt-quatre heures.

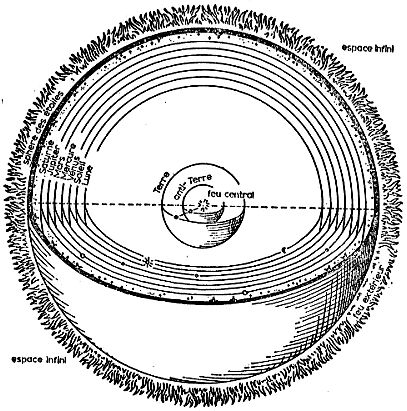
Système cosmologique du pythagorien Philolaos

Plus tard, on suggéra que les sphères intérieures tournaient en sens inverse autour d'un axe incliné de 23,5° sur l'axe des Pôles, la sphère portant le Soleil mettant un an pour une révolution, celle portant la Lune un mois et celle portant Jupiter douze ans.  Ce modèle laissait encore inexpliquées les boucles observées sur les trajectoires des planètes, ou les mouvements quelques peu irréguliers du Soleil et de la Lune. Pour expliquer ceux-ci, le modèle devait être rendu encore plus complexe. Eudoxe, environ 370 av. J.-C. , imagina un système de nombreuses sphères concentriques, disposées comme les tuniques d'un oignon. Quatre de ces sphères, tournant chacune autour d'un axe différent étaient nécessaires pour rendre compte du mouvement d'une seule planète. En tout, il y avait vingt-sept sphères (quatre pour chaque planète, trois pour le Soleil, trois pour la Lune une pour les étoiles fixes).

Ce modèle d'Eudoxe utilisait des sphères simples, de vitesse de rotation constante. Il était en accord avec les observations et permettait de prévoir les positions des planètes. C'était un bon modèle, mais très compliqué.

Les mesures faites par les Grecs.

La mesure du rayon terrestre par Eratosthène de Cyrène :

En 249 av. J.-C. Environ, Eratosthène utilisa le fait que l'on pouvait voir se réfléchir le Soleil dans l'eau d'un puits profond, à Syène (de nos jours Assouan), à midi ; d'autre part, d'après sa propre observation au même moment, la longueur de l'ombre d'un obélisque d'Alexandrie permettait de calculer l'angle des rayons solaires avec la verticale 7,2°. Syène est à 800 km au sud d'Alexandrie ; donc 800 km sur la circonférence de la Terre correspondent à un angle au centre de 7,5°, en supposant que le Soleil soit suffisamment éloigné pour que les rayons atteignant la Terre soient considérés comme parallèles. 

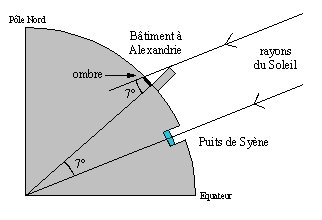
La ville de Syène (aujourd'hui Assouan) se situe à peu près sur le tropique du Cancer. De ce fait, à midi au moment du solstice d'été, le soleil culmine dans le ciel. Pour s'en assurer, Eratosthène attend que le soleil, se trouvant à la verticale, éclaire le fond d'un puits. D'autres sources disent qu'il aurait utilisé un cadran solaire et attendu que l'aiguille cesse de porter une ombre. Ce qui revient au même.

Au même instant, à Alexandrie, ville éloignée de 5000 stades (environ 800 km) une expérience analogue est entreprise. On mesure alors l'ombre d'un obélisque dont on connaît la hauteur afin de calculer l'angle que font les rayons du soleil avec la verticale. On trouve â = 7,2°

Eratosthène considère que le soleil suffisamment éloigné projette des rayons tous parallèles. L'angle â ainsi mesuré est alterne-interne égal à l'angle au centre de la terre interceptant l'arc Alexandrie-Syène.

Un stade valant selon les historiens environ 160m, la circonférence de la terre calculée par Eratosthène est donc environ égale à 40 000 km alors que la circonférence à l'équateur actuellement connue est de 40 075 km. C'est ici un résultat magnifique pour la science hellénique, et très proche de nos propres mesures effectuées avec des instruments modernes.

Article en construction.